Пример решения задачи на растяжение и сжатие

Условие задачи на растяжение и сжатие

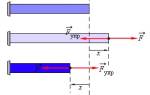
Стальной стержень (модуль Юнга в кН/см²) подвергается внешним осевым силам (см. рис. 3.1). Необходимо построить эпюры продольных сил и нормальных напряжений. Оцените прочность стержня, учитывая предельное напряжение (предел текучести) в кН/см² и допускаемый коэффициент запаса. Также найдите удлинение стержня.

Расчетная схема для задачи на растяжение и сжатие

Решение пример задачи на растяжение и сжатие

Определяем значение опорной реакции , возникающей в заделке

Учитывая это, направим опорную реакцию вниз. Из уравнения равновесия находим: кН.

Строим эпюру продольных сил

Разделим длину стержня на три участка. Границами участков являются сечения, где приложены внешние силы или изменяется размер поперечного сечения.

Используем метод сечений. Сделаем по одному сечению в произвольном месте каждого из трех участков стержня.

Сечение 1 — 1. Закроем верхнюю часть стержня (рис. 3.2, б). Сечение 1 — 1 мысленно считаем неподвижным. Внешняя сила растягивает нижнюю часть стержня, а верхняя часть противодействует этому растяжению. Это противодействие заменим внутренней продольной силой, направленной от сечения и соответствующей растяжению. Разрушение стержня не произойдет, если внутренняя продольная сила в сечении 1 — 1 уравновесит внешнюю силу. Поэтому:

кН.

Сечение 2 — 2. Внешняя сила растягивает нижнюю часть стержня, а сила в сечении 2 — 2 сжимает её (сечение 2 — 2 также считаем неподвижным). Согласно условию задачи, . Чтобы уравновесить эти силы, в сечении 2 — 2 должна возникнуть внутренняя сила , направленная к сечению и противодействующая сжатию. Она равна:

кН.

Сечение 3 — 3. Закроем часть стержня ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю сжимающую силу . Поэтому она направлена к сечению и равна:

кН.

Если мы закроем верхнюю часть стержня, продольная сила также будет противодействовать сжатию и равна:

кН.

При построении эпюры продольных сил будем использовать следующее правило: внутренняя продольная сила считается положительной, если она противодействует растяжению, и отрицательной, если противодействует сжатию. Это позволяет наглядно видеть, какая часть стержня испытывает растяжение, а какая — сжатие. Это важно для стержней из хрупкого материала, у которых допускаемые напряжения на растяжение и сжатие различаются.

Таким образом, в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня наблюдается сжатие, поэтому кН.

Для построения эпюры продольных сил проведем тонкую линию, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе откладываем от этой вертикальной оси, учитывая их знак. В пределах каждого участка стержня продольная сила остается постоянной, поэтому «заштриховываем» горизонтальными линиями соответствующий участок.

Каждая линия «штриховки» (ордината эпюры) в принятом масштабе показывает значение продольной силы в соответствующем поперечном сечении стержня.

Полученную эпюру обводим жирной линией.

Анализируя эпюру, видим, что в местах приложения внешних сил происходит скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Изменение поперечного размера стержня, как видно из рис. 3.2, д, не сказывается на характере эпюры.

Строим эпюру нормальных напряжений

Нормальное напряжение в k-м поперечном сечении стержня при растяжении (или сжатии) вычисляется по формуле:

[ sigmak = frac{N}{Ak} ]

где ( N ) — продольная сила, ( A_k ) — площадь k-го поперечного сечения стержня.

В первом поперечном сечении стержня нормальное напряжение составляет

[ sigma_1 = text{кН/см}^2, ]

во втором —

[ sigma_2 = text{кН/см}^2, ]

в третьем —

[ sigma_3 = text{кН/см}^2. ]

Построим эпюру по вычисленным значениям (рис. 3.2, е). В пределах каждого участка стержня напряжения постоянны, поэтому эпюра напряжений параллельна оси. Обратите внимание, что в отличие от эпюры N, «скачок» на эпюре напряжений наблюдается не только в местах приложения внешних сил, но и там, где изменяется размер поперечного сечения стержня.

Оцениваем прочность стержня

Сравниваем максимальное (по модулю) нормальное напряжение во втором сечении стержня с допустимым напряжением. Допустимое напряжение — это доля предельного напряжения, при котором начинается разрушение материала. Для стали, как пластичного материала, предельное напряжение соответствует пределу текучести.

Таким образом, имеем:

кН/см².

Условие прочности записывается как:

кН/см² > кН/см².

Это означает, что прочность стержня на втором участке не обеспечена.

Следовательно, необходимо увеличить площадь поперечного сечения стержня на втором участке, которая составляет см².

Анализ показывает, что на других участках стержня условие прочности выполняется.

Определяем требуемую площадь поперечного сечения стержня на втором участке:

см².

Принимаем на втором участке см².

Вычисляем удлинение всего стержня

При переменных значениях продольной силы и площади поперечного сечения удлинение стержня вычисляется по формуле

,

где E — модуль Юнга, а — длина участка стержня.

Таким образом, длина стержня уменьшается на мм.

Задача по сопромату на растяжение и сжатие для самостоятельного решения

Схемы для задачи на растяжение и сжатие

Исходные данные к задаче на растяжение и сжатие

Номер схемы	F, см²	a, м	b, м	c, м	P, кН
1	2,0	1,2	1,4	1,6	11
2	2,2	1,4	1,6	1,4	12
3	2,4	1,8	1,6	1,2	13
4	2,6	1,6	2,0	1,0	14
5	2,8	2,0	1,8	1,2	15
6	3,0	2,2	1,6	1,4	16
7	3,2	2,4	1,4	1,6	17
8	3,4	2,6	1,2	1,8	18
9	3,6	2,8	1,0	1,4	19
10	3,8	2,4	1,6	1,2	20

ПроСопромат.ру

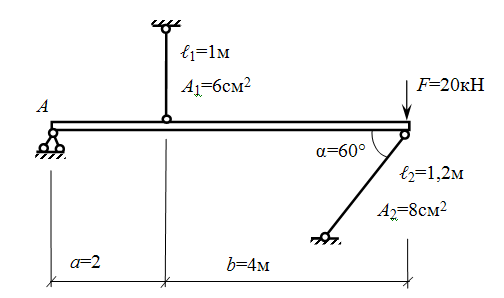
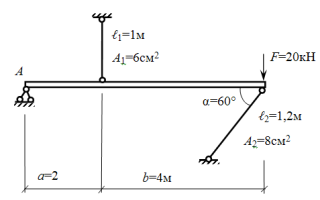
Задача: определить напряжение в стальных стержнях, поддерживающих абсолютно жесткую балку. Материал — сталь Ст3, α=60°, [σ]=160 МПа.

1. Вычерчиваем схему в масштабе и нумеруем стержни.

В шарнирно-неподвижной опоре А возникают реакции RА и НА. В стержнях 1 и 2 возникают усилия N1 и N2. Применим метод сечений, вырезав среднюю часть системы. Жесткую балку покажем схематично — линией, а усилия N1 и N2 направим от сечения.

Составляем уравнения равновесия.

Количество неизвестных превышает количество уравнений статики на 1, что делает систему статически неопределимой. Для решения потребуется одно дополнительное уравнение, которое можно получить, рассмотрев схему деформации системы. Шарнирно-неподвижная опора А остается на месте, а стержни деформируются под действием силы.

Схема деформаций.

Составим условие совместности деформаций, рассматривая подобие треугольников АСС1 и АВВ1. Из подобия треугольников АВВ1 и АСС1 запишем соотношение:

где ВВ1=Δℓ1 (удлинение первого стержня).

Теперь выразим СС1 через деформацию второго стержня. Укрупним фрагмент схемы.

Из рисунка видно, что СС2 = СС1·cos (90º-α) = СС1·sinα.

Но СС2 = Δℓ2, тогда Δℓ2 = СС1·sinα, откуда:

Превратим условие совместности деформации в уравнение совместности, используя формулу Гука для деформаций. Учитываем характер деформаций: укорочение со знаком «-», удлинение со знаком «+».

Тогда уравнение совместности деформаций будет:

Сокращаем обе части на E, подставляем числовые значения и выражаем N1 через N2.

Подставим соотношение в уравнение, откуда найдем:

N1 = 7,12 кН (растянут),
N2 = -20,35 кН (сжат).

Определим напряжения в стержнях. Задача решена.

Расчет бруса с зазором. Для статически неопределимого стального ступенчатого бруса построим эпюры продольных сил, нормальных напряжений и перемещений. Проверим прочность бруса. До нагружения между верхним концом и опорой был зазор Δ=0,1 мм. Материал — сталь Ст3, модуль продольной упругости E=2·10^5 МПа, допускаемое напряжение [σ]=160 МПа.

1. После нагружения зазор закроется, и реакции возникнут как в нижней, так и в верхней опоре. Обозначим их как RA и RB. Составим уравнение статики:

∑у=0: RA — F1 + F2 — RB = 0.

В уравнении 2 неизвестных, а уравнение одно, значит задача статически неопределима, и для ее решения требуется 1 дополнительное уравнение.

Это уравнение совместности деформаций. В данном случае изменение длины бруса (удлинение) не может превышать величину зазора, т.е. Δℓ=Δ — это условие совместности деформации.

1. Разобьем брус на участки и проведем на них сечения — их 4 по количеству характерных участков. Каждое сечение рассматриваем отдельно, двигаясь от нижней опоры вверх. В каждом сечении выражаем силу N через неизвестную реакцию. Направляем N от сечения.

Выписываем значения продольных сил в сечениях:

N1 = — RA,
N2 = 120 — RA,
N3 = 120 — RA,
N4 = 30 — RA.

3. Возвращаемся к условию совместности деформации. Имеем 4 участка, значит:

Δℓ1 + Δℓ2 + Δℓ3 + Δℓ4 = Δ (величина зазора).

Используя формулу Гука для определения абсолютной деформации, составим уравнение совместности деформаций — это дополнительное уравнение, необходимое для решения задачи.

Упрощаем уравнение. Величина зазора Δ=0,1 мм = 0,1·10^-3 м.

E — модуль упругости, E=2·10^5 МПа=2·10^8 кПа.

Подставляем вместо N их значения, записанные через опорную реакцию RA.

4. Вычисляем N и строим эпюру продольных сил:

N1 = — RA = -47,5 кН,
N2 = 120 — RA = 72,5 кН,
N3 = 120 — RA = 72,5 кН,
N4 = 30 — RA = -17,5 кН.

5. Определяем нормальные напряжения σ по формуле и строим их эпюры.

Строим эпюру нормальных напряжений.

Проверяем прочность:

σmax = 90,63 МПа < [σ] = 160 МПа.

Прочность обеспечена.

1. Вычисляем перемещения, используя формулу Гука для деформаций.

Идем от стены А к зазору.

Получили величину ω4, равную зазору, что подтверждает правильность определения перемещений.

Строим эпюру перемещений.

Задача решена.

Для статически определимого стального ступенчатого бруса построим эпюры продольных сил, нормальных напряжений и перемещений. Проверим прочность бруса. Материал — сталь Ст3, модуль продольной упругости E=2·10^5 МПа, допускаемое напряжение [σ]=160 МПа.

1. Произвольно направляем реакцию стены RA и определяем её из уравнения равновесия:

∑у=0: — RA + F3 — F2 + F1 = 0.

RA = F3 — F2 + F1 = 60 — 25 + 10 = 45 кН.

1. Определяем продольные силы N методом сечений. Сечения расставляем на характерных участках. В нашей задаче их 6. Каждое сечение рассматриваем отдельно. Силу N направляем от сечения.

Строим эпюру N. Все значения откладываем перпендикулярно от нулевой линии в выбранном масштабе.

Положительные значения откладываем вправо от нулевой линии, отрицательные — влево.

1. Определяем нормальные напряжения σ в сечениях по формуле. Внимательно смотрим, по какой площади проходит сечение.

Строим эпюру σ.

Проверяем прочность по условию:

|σmax| = 75 МПа < [σ] = 160 МПа.

Прочность обеспечена.

4. Определяем перемещение бруса.

Расчет ведется от стены, в которой перемещение равно нулю (ωА = 0).

Формула Гука для определения абсолютной деформации участка.

Определяем перемещения:

Строим эпюру перемещений ω.

Задача решена.

На стальной стержень действует продольная сила P и собственный вес (γ = 78 кН/м³). Найти перемещение сечения 1-1.

Дано: E = 2·10^5 МПа, A = 11 см², a = 3,0 м, b = 3,0 м, c = 1,3 м, P = 2 кН.

Учет собственного веса.

Перемещение сечения 1-1 складывается из перемещения от действия силы P, от собственного веса выше сечения и от собственного веса ниже сечения. Перемещение от действия силы P будет равно удлинению участка стержня длиной b + a, расположенного выше сечения 1-1. Нагрузка P вызывает удлинение только участка a, так как только на нем имеется продольная сила от этой нагрузки. Согласно закону Гука, удлинение от действия силы P будет равно:

Определим удлинение от собственного веса стержня ниже сечения 1-1. Обозначим его как . Оно будет вызвано собственным весом участка c и весом стержня на участке a + b.

Определим удлинение от собственного веса стержня выше сечения 1-1. Обозначим его как . Оно будет вызвано собственным весом участка a + b.

Тогда полное перемещение сечения 1-1:

Сечение 1-1 опустится на 0,022 мм.

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу Q; 2) найти допускаемую нагрузку Qдоп, приравняв большее из напряжений в двух стержнях к допускаемому напряжению; 3) найти предельную грузоподъемность системы, если предел текучести; 4) сравнить обе величины, полученные при расчете по допускаемым напряжениям и предельным нагрузкам. Размеры: a = 2,1 м, b = 3,0 м, c = 1,8 м, площадь поперечного сечения A = 20 см².

Данная система один раз статически неопределима. Для раскрытия статической неопределимости необходимо решить совместно уравнение равновесия и уравнение совместности деформаций стержней.

(1) — уравнение равновесия.

Составим деформационную схему. Тогда из схемы:

(2)

По закону Гука имеем:

Длины стержней: тогда получим:

Подставим полученное соотношение в уравнение (1).

Определяем напряжение в стержнях.

Допускаемая нагрузка:

В предельном состоянии: подставим полученные соотношения в уравнение (1).

При сравнении видим увеличение нагрузки.

Колонна, состоящая из стального стержня и медной трубы, сжимается силой P. Длина колонны ℓ. Выразить усилия и напряжения, возникающие в стальном стержне и медной трубе. Проведем сечение 1-1 и рассмотрим равновесие отсеченной части.

Составим уравнение статики: NC + NM — P = 0, NC + NM = P (1).

Задача статически неопределима. Уравнение совместности деформации запишем из условия, что удлинения стального стержня и медной трубы одинаковы:

(2).

Сократим обе части на длину стержня и выразим усилие в медной трубе через усилие в стальном стержне:

(3).

Подставим найденное значение в уравнение (1).

При совместной работе всегда сильнее напряжен элемент из материала с большим модулем упругости. При ЕС = 2·10^5 МПа, ЕМ = 1·10^5 МПа:

Для колонны определим напряжения на всех участках. После приложения силы P зазор закрывается, P = 200 кН, E = 2·10^5 МПа, A = 25 см². После приложения силы P возникнут усилия в защемлениях. Обозначим их как C и B.

Составим уравнение статики: ∑y = 0; C + B — P = 0; (1).

Дополнительное уравнение совместности деформаций: ∆ℓ1 + ∆ℓ2 = 0,3 мм (2).

Чтобы найти абсолютную деформацию, необходимо знать продольную силу на участке. На первом участке продольная сила равна C, на втором — разности (C — P). Подставим эти значения в выражения абсолютных деформаций:

(3).

Подставляем выражение (3) в выражение (2) и находим: C = 150 кН, а из (1) B = 50 кН.

Тогда напряжения на участках:

На трех стальных стержнях подвешена жесткая балка; стержень 2 выполнен короче проектного. Определить напряжения в стержнях после сборки системы. Дано:

Схема заданной системы.

После завершения сборки в данной системе жесткая балка повернется и займет новое положение.

Схема деформирования.

Точки С, D и К переместятся в положения С1, D1 и К1.

Согласно картине деформирования, СС1 = Δℓ1, DD1 = Δ — D1D2 = Δ — Δℓ2, KK1 = Δℓ3. При этом стержни 1 и 3 испытывают сжатие, а стержень 2 — растяжение.

В соответствии со схемой деформирования уравнение равновесия примет вид:

Дополнительные уравнения можно получить на основе анализа схемы деформирования. Из подобия треугольников ВСС1 и BDD1, треугольников ВСС1 и BKK1 следует:

Согласно закону Гука абсолютные деформации:

Тогда дополнительные уравнения запишутся следующим образом. Решая совместно данную систему полученных дополнительных уравнений и уравнение равновесия, получим:

N1 = 14,3 кН (стержень сжат),
N2 = 71,5 кН (стержень растянут),
N3 = 42,9 кН (стержень сжат).

Таким образом, искомые напряжения в стержнях имеют значения: задача решена.

Ступенчатый медный стержень нагревается от температуры tН=20ºС до tК=50ºС. Проверить прочность стержня. Дано:

Составим уравнение равновесия стержня, предположив замену внешних связей реактивными силами. Система статически неопределима, и для ее решения требуется дополнительное уравнение.

Уравнение совместности деформаций следует из условия, что перемещения внешних связей равны 0 — WВ=0 или WК=0. Таким образом:

Откуда:

В результате RB = 20723 Н.

Нормальные силы и напряжения на участках:

Согласно результатам расчетов σmax = |69,1| МПа, при этом σmax < σadm (69,1 < 80). Следовательно, условие прочности стержня выполняется.

Расчет стержня с зазором. Для стального ступенчатого стержня при наличии зазора между нижним торцом и опорой требуется построить эпюры нормальных сил, напряжений и перемещений; проверить прочность. Дано:

Схема стержня; эпюры нормальных сил, напряжений и перемещений.

Составим уравнение равновесия стержня:

В нем два неизвестных, система один раз статически неопределима, требуется дополнительное уравнение — уравнение деформаций.

Дополнительное уравнение можно записать из условия закрытия зазора в процессе деформирования стержня:

Для рассматриваемых участков их абсолютные деформации:

Определим нормальные (продольные) силы методом сечений, идем от стены к зазору:

Подставим все найденные значения в дополнительное уравнение:

После подстановки исходных данных и сокращений:

Из уравнения равновесия получаем:

Таким образом, RB = 40,74 кН, RK = 9,26 кН.

Расчет нормальных сил: строим эпюру N.

Расчет нормальных напряжений: строим эпюру нормальных напряжений.

Расчет перемещений характерных сечений.

Принимается правило знаков для перемещений: вниз — положительные, вверх — отрицательные. Строим эпюру перемещений.

Из эпюры нормальных напряжений видно, что:

Следовательно, условие прочности стержня не выполняется.

Навигация по записям

Литература:

1. М.П. Киселева, З.С. Смирнова, Л.М. Борисова и др. Поиск новых противоопухолевых соединений среди производных N-гликозидов индоло[2,3-а] карбазолов // Российский онкологический журнал. 2015. № 1. С. 33-37.
2. Ковнер. Очерки истории M.
3. Bangun H., Aulia F., Arianto A., Nainggolan M. Preparation of mucoadhesive gastroretentive drug delivery system of alginate beads containing turmeric extract and anti-gastric ulcer activity. Asian Journal of Pharmaceutical and Clinical Research. 2019; 12(1): 316–320. DOI: 10.22159/ajpcr.2019.v12i1.29715.
4. Задачи по растяжению и сжатию.
5. Задачи по растяжению и сжатию.
6. Wise. Review of the History of Medicine. Л., 1967.
7. Moustafine R. I., Bukhovets A. V., Sitenkov A. Y., Kemenova V. A., Rombaut P., Van den Mooter G. Eudragit® E PO as a complementary material for designing oral drug delivery systems with controlled release properties: comparative evaluation of new interpolyelectrolyte complexes with countercharged Eudragit® L 100 copolymers. Molecular Pharmaceutics. 2013; 10(7): 2630–2641. DOI: 10.1021/mp4000635.