Деформация растяжения — это деформация, возникающая при продольном приложении нагрузки к телу, параллельно его точкам крепления. Примером служит буксировочный трос: при движении он выпрямляется и тянет буксируемый объект. Если нагрузка не превышает предельные значения, трос восстанавливает свою форму после снятия нагрузки.

Деформация растяжения — важное лабораторное исследование физических свойств материалов. При приложении растягивающих напряжений определяются:

1. Упругая деформация — материал восстанавливает первоначальное состояние.
2. Пластическая деформация — материал не восстанавливает первоначальное состояние.
3. Разрушение на пределе прочности.

Эти испытания критичны для тросов и веревок, используемых в строповке, креплении грузов и альпинизме. Растяжение также важно при строительстве подвесных систем.

Деформация сжатия — аналог растяжения, но нагрузка прикладывается к телу. Сжатие с двух сторон уменьшает длину объекта и увеличивает его прочность, при больших нагрузках возникают утолщения типа «бочка». Деформация сжатия широко применяется в металлургии, где металл получает повышенную прочность и устраняются дефекты структуры. Она также важна в строительстве, так как все элементы конструкции испытывают давящие нагрузки.

Деформация сдвига — это деформация, при которой нагрузка прикладывается параллельно основанию тела. В результате одна плоскость смещается относительно другой. Все крепежные элементы, такие как болты и гвозди, испытываются на предельные нагрузки сдвига. Пример — расшатанный стул, где пол — основание, а сиденье — плоскость нагрузки.

Деформация изгиба — это деформация, при которой нарушается прямолинейность главной оси тела. Все тела, подвешенные на опорах, испытывают изгиб. Твердые тела могут выдерживать не только свой вес, но и дополнительные нагрузки. Различают чистый и косой изгиб в зависимости от приложения нагрузки. Значение деформации изгиба критично для проектирования упругих конструкций, таких как мосты и оси автомобилей.

Деформация кручения — это деформация, возникающая при приложении крутящего момента, вызванного парой сил, действующих перпендикулярно оси тела. Кручение характерно для валов машин и пружин.

Закон Гука — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году Робертом Гуком. Закон гласит, что сила упругости, возникающая при деформации, прямо пропорциональна величине этой деформации.

Для тонкого растяжимого стержня закон Гука записывается как:

[ F = k cdot Delta l ]

где ( F ) — сила, ( Delta l ) — абсолютное удлинение (или сжатие), ( k ) — коэффициент упругости.

Коэффициент упругости зависит от свойств материала и размеров стержня. Его можно выразить через модуль упругости первого рода или модуль Юнга, который является механической характеристикой материала.

При введении относительного удлинения и нормального напряжения закон Гука в относительных единицах записывается как:

[ sigma = E cdot varepsilon ]

где ( sigma ) — нормальное напряжение, ( E ) — модуль Юнга, ( varepsilon ) — относительное удлинение.

Модуль Юнга — физическая величина, характеризующая сопротивление материала растяжению или сжатию при упругой деформации. Он измеряется в ньютонах на квадратный метр или паскалях.

Модуль Юнга рассчитывается по формуле:

[ E = frac{F cdot l}{S cdot x} ]

где ( F ) — сила, ( S ) — площадь, ( l ) — длина стержня, ( x ) — изменение длины стержня.

С помощью модуля Юнга можно вычислить скорость распространения продольной волны в тонком стержне:

[ v = sqrt{frac{E}{rho}} ]

где ( rho ) — плотность вещества.

Деформация растяжения-сжатия

В машиностроении, строительстве и архитектуре для расчета прочности и жесткости материалов применяется математический аппарат технической механики. Деформация растяжения — ключевое понятие, описывающее механические процессы в материалах под воздействием внешних сил. Для наглядности рассматриваются изменения в брусе с постоянным сечением, характерные для упругой деформации.

Закон Гука (английский физик Р. Гук, 1653-1703) утверждает, что нормальное напряжение линейно зависит от относительного удлинения или укорочения. Эта зависимость описывается формулой:

Коэффициент пропорциональности E (модуль упругости, модуль Юнга) определяет жесткость материала и измеряется в паскалях (ПА).

Значения модуля упругости установлены эмпирически для большинства конструкционных материалов и могут быть найдены в справочниках по машиностроению. Относительная деформация — это отношение изменения длины бруса к его первоначальным размерам, безразмерная величина, иногда выражаемая в процентах.

При растяжении или сжатии у бруса изменяется не только длина, но и поперечные размеры: при сжатии происходит утолщение, а при растяжении толщина сечения уменьшается. Эти изменения находятся в линейной зависимости друг от друга. Коэффициент пропорциональности Пуассона (французский ученый С. Пуассон, 1781-1840) остается постоянным для данного материала.

Внутренние усилия при растяжении и сжатии

При приложении внешних нагрузок к брусу с постоянным сечением, направленных параллельно его центральной оси и перпендикулярно сечению, происходят деформации: растяжение или сжатие. На основе гипотезы о независимости внешнего воздействия для каждого поперечного сечения можно рассчитать внутренние усилия как векторную сумму всех приложенных внешних сил. Растягивающие нагрузки считаются положительными, а сжимающие — отрицательными.

Рассматривая произвольное сечение бруса или стержня, можно утверждать, что внутренние напряжения равны векторной сумме всех внешних сил, действующих с одной стороны. Это справедливо с учетом принципа Сен-Венана о смягчении граничных условий, поскольку распределение внутренних усилий по поверхности разреза имеет сложный характер. Однако в данном случае погрешность можно считать несущественной.

Применяя гипотезу Бернулли о плоских сечениях, можно построить эпюры для наглядного представления распределения сил и напряжений по центральной оси бруса. Графическое представление позволяет быстро определить наиболее нагруженные участки стержня и сосредоточить расчеты на критических точках.

Все вышесказанное применимо при квазистатической нагрузке стержня с постоянным диаметром. Потенциальная энергия системы при растяжении стержня определяется формулой:

U = W = FΔl/2 = N²l/(2EA)

Потенциальная энергия растяжения U накапливается в образце и равна выполненной работе W, произведенной силой F для увеличения длины стержня на величину абсолютного удлинения. Преобразовав формулу, можно вычислить потенциальную энергию растяжения, рассчитав отношение квадрата продольной силы N, умноженной на длину стержня l, к удвоенному произведению модуля Юнга E материала и площади сечения A.

Энергия растяжения всегда положительна, и гипотезу о независимости действия сил применить нельзя, так как это не векторная величина. Единица измерения — джоуль (Дж). В нижней части формулы находится произведение EA — жесткость сечения, которая при неизменном модуле Юнга увеличивается только за счет площади. Отношение жесткости к длине бруса рассматривается как жесткость всего бруса.

Напряжения при растяжении сжатии

Используя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех внутренних усилий, распределенных по сечению. Гипотеза Бернулли и предположение о ненадавливании волокон позволяют утверждать, что напряжение σ в любой точке разреза будет постоянным, так как реакция продольных волокон одинакова на всем поперечном сечении. Для вычисления нормального напряжения σ используется формула:

Напряжение для упруго деформированного стержня определяется как отношение внутренней силы N к площади сечения A. Оно считается положительным при растяжении и отрицательным при сжатии.

Абсолютная деформация зависит от жесткости сечения, величины продольной силы и длины бруса. Это можно выразить формулой:

Δl = Nl / EA

Методика расчета абсолютного изменения длины заключается в вычислении отношения продольной силы N, умноженной на длину стержня l, к жесткости сечения (произведению модуля Юнга E и площади сечения A).

В реальных расчетах на брус действуют различные разнонаправленные силы. Для решения таких задач необходимо строить эпюры, которые наглядно показывают напряжения на разных участках и причины деформации при растяжении и сжатии.

В квазистатической системе, такой как брус или стержень с переменным сечением или отверстием, потенциальная энергия растяжения рассматривается как сумма энергий однородных участков. При расчетах важно правильно разделить стержень на участки и смоделировать все действующие силы и напряжения. Построение эпюр в реальных расчетах — сложная задача, требующая от инженера глубокого понимания нагрузок, действующих на деталь. Например, вал со шкивами разного диаметра требует определения критических точек и разбивки на соответствующие участки, а затем построения графиков по ним.

Деформации при растяжении сжатии

При растяжении или сжатии бруса возникают два вида деформации: упругая и пластическая. Упругая деформация восстанавливает первоначальные параметры после прекращения воздействия, тогда как при пластической деформации материал теряет форму и размеры. Предел текучести — это величина воздействия, при которой происходит переход от упругой к пластической деформации.

Для расчета перемещения при растяжении бруса или стержня используется метод разделения на участки, где прикладываются внешние силы. В точках приложения силы вычисляется изменение длины по формуле: Δl = Nl / EA. Эта формула зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговое перемещение бруса — это сумма всех частичных перемещений, рассчитанных для точек приложения силы.

Поперечные деформации бруса, проявляющиеся в утолщении при сжатии и истончении при растяжении, также характеризуются абсолютной и относительной величиной. Абсолютная деформация — это разница между размерами сечения до и после приложения силы, а относительная — отношение абсолютной деформации к исходному размеру. Коэффициент Пуассона, отражающий зависимость продольной и поперечной деформаций, определяет упругие свойства материалов и остается неизменным при растяжении и сжатии. Продольные деформации наиболее наглядно демонстрируют процессы, происходящие в брусе или стержне под внешним воздействием. Зная величину одной из деформаций и используя коэффициент Пуассона, можно рассчитать значение неизвестной.

Для определения деформации пружины при растяжении применяется закон Гука:

F = kx

где x — увеличение длины пружины, k — коэффициент жесткости (измеряется в Н/м), F — сила упругости, направленная в противоположную от смещения сторону. Абсолютная деформация равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала и может помочь в выборе материала для решения конкретной задачи.

Расчеты на прочность и жесткость

Прочность характеризует способность конструкционного материала противостоять внешним воздействиям без разрушений и остаточных изменений. Жесткость зависит от модуля Юнга и размера сечения: чем больше площадь сечения при неизменном модуле упругости, тем выше жесткость. Жесткость подразумевает способность материала деформироваться без значительных изменений. Коэффициент запаса прочности — безразмерная величина, равная отношению предельного напряжения к допустимому. Он показывает, насколько конструкция может выдерживать случайные и непредусмотренные нагрузки. Пластические материалы имеют наименьший запас прочности (1.2-2.5), хрупкие — (2-5).

Использование этих коэффициентов позволяет рассчитывать опасную толщину стержня, при которой может возникнуть максимальное нормальное напряжение. С помощью коэффициента прочности и предельного напряжения можно определить необходимый диаметр вала, который обеспечит упругую деформацию и предотвратит пластическую. Для инженеров-экономистов важны расчеты минимально безопасных размеров деталей конструкции при заданных нагрузках.

Большинство практических расчетов на прочность и жесткость направлены на получение минимальных значений геометрических размеров конструкционных элементов и деталей машин с учетом известных внешних воздействий и необходимого запаса прочности. Также можно решать обратные задачи, определяя предельные нагрузки при фиксированных геометрических размерах и конкретном материале.

Сложные конструкции делят на элементарные части для расчетов, а затем интерпретируют результаты для всей системы. Для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений в статически определенной системе.

Зная жесткость материала, можно рассчитать максимально возможную длину балки или стержня при неизменном сечении. Для ступенчатых валов строят эпюры воздействия внешних сил и внутренних напряжений в критических точках. Правильная теоретическая модель влияет на долговечность вала и его устойчивость к динамическим крутящим моментам. На этапе проектирования можно выявить слабые места и рассчитать необходимые параметры для заданного предела прочности.

При расчетах на прочность учитываются такие понятия, как срез и смятие. Срез проявляется в разрушении детали соединения при наличии достаточной силы, действующей перпендикулярно к поперечному сечению.

При расчетах соединений используют пределы текучести материалов и коэффициенты запаса прочности для вычисления максимально возможных напряжений.

Исследования на прочность обычно включают несколько задач: проверка прочности при известных усилиях и площади сечения для оценки фактического коэффициента запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисление грузоподъемности или несущей способности через определение внутреннего усилия при известной площади сечения и напряжении.

Прочностные расчеты в условиях условно статических систем сложны и требуют учета множества факторов. Их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.

Деформация растяжения-сжатия — характеристики, расчеты, параметры

Процесс деформации твердого тела — это изменение его формы под действием внешней нагрузки. Каждый твердый материал имеет кристаллическую структуру с определенным расположением атомов и частиц. При приложении нагрузки происходит смещение отдельных элементов или целых слоев, что приводит к возникновению дефектов в материале.

Внутренние усилия при растяжении-сжатии

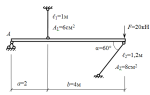
Осевое (центральное) растяжение или сжатие прямого бруса возникает под действием внешних сил, направленных вдоль оси бруса. При этом в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в определённом сечении равна алгебраической сумме проекций всех внешних сил, действующих с одной стороны от этого сечения. По правилу знаков, положительные продольные силы N возникают от растягивающих нагрузок, а отрицательные — от сжимающих (рис. 5).

Для определения участков стержня или его сечений с максимальным значением продольной силы строят эпюру продольных сил, используя метод сечений, подробно описанный в статье:

Анализ внутренних силовых факторов в статистически определимых системах.

Рекомендую также ознакомиться с статьёй:

Расчёт статистически определимого бруса.

Изучив теорию и задачи по указанным ссылкам, вы сможете глубже понять тему «Растяжение-сжатие».

Виды деформации твердых тел

Деформация растяжения

Деформация растяжения — это деформация, возникающая при приложении нагрузки вдоль тела, параллельно точкам его крепления. Наиболее наглядно растяжение можно продемонстрировать на буксировочном тросе для автомобилей. Трос крепится в двух точках: к буксиру и буксируемому объекту. При начале движения трос выпрямляется и начинает тянуть буксируемый объект. Если нагрузка не превышает предельные значения, трос, находясь в натянутом состоянии, восстанавливает свою форму после снятия нагрузки.

Деформация растяжения — одно из основных лабораторных исследований физических свойств материалов. При приложении растягивающих напряжений определяются величины, при которых материал способен:

1. воспринимать нагрузки с восстановлением первоначального состояния (упругая деформация);
2. воспринимать нагрузки без восстановления первоначального состояния (пластическая деформация);
3. разрушаться на пределе прочности.

Эти испытания важны для всех тросов и веревок, используемых в строповке, креплении грузов и альпинизме. Растяжение также имеет значение при строительстве сложных подвесных систем со свободными рабочими элементами.

Деформация сжатия

Деформация сжатия — это вид деформации, аналогичный растяжению, но с отличием в способе приложения нагрузки: она прикладывается соосно и направлена к телу. Сжатие объекта с двух сторон уменьшает его длину и одновременно приводит к упрочнению. При больших нагрузках в материале могут образовываться утолщения типа «бочка».

Деформация сжатия широко применяется в металлургии, особенно в процессе ковки, где металл приобретает повышенную прочность и устраняет дефекты структуры. Также сжатие играет важную роль в строительстве: все элементы конструкции фундамента, свай и стен испытывают давящие нагрузки. Правильный расчет несущих конструкций позволяет сократить расход материалов без потери прочности.

Деформация сдвига

Деформация сдвига — это деформация, возникающая при приложении нагрузки параллельно основанию тела. В результате одна плоскость тела смещается относительно другой. Все крепежные элементы, такие как болты, шурупы и гвозди, испытывают предельные нагрузки сдвига. Простой пример деформации сдвига — расшатанный стул, где пол служит основанием, а сидение — плоскостью приложения нагрузки.

Схема сдвига образца

Посмотрите прибор, измеряющий деформацию сдвига →

Деформация изгиба

Деформация изгиба — это изменение формы, при котором нарушается прямолинейность главной оси тела. Все тела, подвешенные на одной или нескольких опорах, испытывают деформации изгиба. Каждый материал может выдерживать определенный уровень нагрузки. Твердые тела обычно справляются не только с собственным весом, но и с дополнительной нагрузкой. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.

Значение деформации изгиба критично для проектирования упругих конструкций, таких как мосты с опорами, гимнастические брусья, турники, оси автомобилей и другие.

Деформация кручения

Деформация кручения — это деформация, возникающая при приложении к телу крутящего момента, вызванного парой сил, действующих в плоскости, перпендикулярной оси тела. Кручение испытывают валы машин, шнеки буровых установок и пружины.

Схема кручения образца

Посмотрите прибор, измеряющий деформацию кручения →

Напряжения при растяжении-сжатии

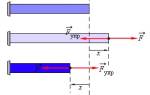
Продольная сила N, определенная методом сечений, является равнодействующей внутренних усилий, распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.

Чтобы определить нормальные напряжения в любой точке бруса, необходимо знать закон их распределения по поперечному сечению. Экспериментальные исследования показывают, что если на поверхность стержня нанести ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии остаются параллельными (рис. 6, а). Это явление описывается гипотезой плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, напряжения в поперечном сечении также одинаковы. Эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис. 6, б. Напряжения равномерно распределены по поперечному сечению, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения в поперечных сечениях растянутого или сжатого бруса равны отношению продольной силы к площади поперечного сечения. Нормальные напряжения считаются положительными при растяжении и отрицательными при сжатии.

Пластическая и упругая деформация

В процессе деформации важна величина межатомных связей. Приложение нагрузки, достаточной для их разрыва, приводит к необратимым последствиям (пластическая деформация). Если нагрузка не превышает допустимые значения, тело может вернуться в исходное состояние (упругая деформация). Примером поведения материалов при этих типах деформации служат резиновый мяч и кусок пластилина. Резиновый мяч обладает упругостью: при падении он сжимается, а затем, преобразовав энергию движения в тепловую и потенциальную, восстанавливает свою форму. Пластилин, обладая высокой пластичностью, при ударе о поверхность необратимо теряет свою первоначальную форму.

Все известные материалы имеют деформационные способности, что обеспечивает им полезные свойства: пластичность, хрупкость, упругость, прочность и другие. Исследование этих свойств важно для выбора или изготовления необходимых материалов. Кроме того, детектирование деформации часто необходимо в приборостроении, для чего используются специальные датчики — экстензометры или тензометры.

Деформации при растяжении-сжатии

Рассмотрим деформации, возникающие при растяжении и сжатии стержня (рис. 6, а). Под действием силы F брус удлиняется на величину Δl, называемую абсолютным удлинением или абсолютной продольной деформацией. Она равна разности длины бруса после деформации l1 и его длины до деформации l.

Отношение абсолютной продольной деформации Δl к первоначальной длине l называется относительным удлинением или относительной продольной деформацией. При растяжении продольная деформация положительна, а при сжатии — отрицательна. Для большинства конструкционных материалов в стадии упругой деформации выполняется закон Гука, который устанавливает линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости E, также называемый модулем упругости первого рода, является коэффициентом пропорциональности между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).

Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации. Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Экспериментально установлено, что в пределах действия закона Гука поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации или коэффициентом Пуассона μ.

На упругой стадии нагружения любого материала значение μ = const, и для различных материалов коэффициент Пуассона находится в пределах от 0 до 0,5 (табл. 2).

Таблица 2
Коэффициент Пуассона

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N. Данная формула позволяет вычислить абсолютное удлинение участка стержня длиной l при условии, что продольная сила в этом участке постоянна. Если продольная сила N изменяется, Δl определяют интегрированием в пределах этого участка.

Произведение (E·A) называют жесткостью сечения стержня при растяжении или сжатии.

Механические свойства материалов

Основные механические свойства материалов при деформации включают прочность, пластичность, хрупкость, упругость и твердость.

Прочность — способность материала сопротивляться внешним силам без разрушения и остаточных деформаций.

Пластичность — свойство материала выдерживать значительные остаточные деформации без разрушения. Остаточные деформации, сохраняющиеся после снятия нагрузки, называются пластическими.

Хрупкость — свойство материала разрушаться при малых остаточных деформациях (например, чугун, бетон, стекло).

Идеальная упругость — способность материала полностью восстанавливать форму и размеры после устранения причин деформации.

Твердость — способность материала сопротивляться проникновению других тел.

Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длиной ( l0 ) и постоянным поперечным сечением площади ( A0 ) статически растягивается с обоих торцов силой ( F ).

Диаграмма сжатия стержня представлена на рисунке 10, а.

Где ( Delta l = l — l0 ) — абсолютное удлинение стержня; ( varepsilon = Delta l / l0 ) — относительное продольное удлинение; ( sigma = F / A0 ) — нормальное напряжение; ( E ) — модуль Юнга; ( sigmap ) — предел пропорциональности; ( sigmau ) — предел упругости; ( sigmat ) — предел текучести; ( sigmav ) — предел прочности (временное сопротивление); ( varepsilon{ост} ) — остаточная деформация после снятия нагрузки. Для материалов без ярко выраженной площадки текучести вводят условный предел текучести ( sigma{0,2} ) — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение диаметра («шейка»). Дальнейшее удлинение происходит в зоне шейки (зона местной текучести). При достижении предела текучести ( sigmat ) поверхность стержня становится матовой — на ней появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии

Опасным сечением при растяжении и сжатии называют поперечное сечение бруса, где возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт для пластических материалов и σпред = σв для хрупких); — коэффициент запаса прочности. Для пластических материалов он составляет 1,2–2,5; для хрупких — 2–5, а для древесины — 8–12.

Расчеты на прочность при растяжении и сжатии

Цель расчета конструкции — оценить ее эксплуатационную пригодность при минимальных затратах материала. Это отражается в методах расчета прочности и жесткости.

Условие прочности стержня при растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня.

Для определения допускаемой нагрузки рассчитывается допускаемая нормальная сила.

Расчет на жесткость при растяжении и сжатии

Работоспособность стержня определяется его предельной деформацией. Абсолютное удлинение стержня должно соответствовать определённому условию.

Часто дополнительно рассчитывают жесткость отдельных участков стержня.

Следующая важная тема теории — изгиб балки.

Литература:

1. Daremberg, «Histoire des sciences médicales» (П., 1966).
2. Patil H., Tiwari R. V., Repka M. A. Recent advancements in mucoadhesive floating drug delivery systems: A mini-review. Journal of Drug Delivery Science and Technology. 2016; 31: 65–71. DOI: 10.1016/j.jddst.2015.12.002.
3. Moustafine R. I., Bobyleva V. L., Bukhovets A. V., Garipova V. R., Kabanova T. V., Kemenova V. A., Van den Mooter G. Structural transformations during swelling of polycomplex matrices based on countercharged (meth)acrylate copolymers (Eudragit® EPO/Eudragit® L 100-55). Journal of Pharmaceutical Sciences. 2011; 100:874–885. DOI:10.1002/jps.22320.
4. Студопедия.
5. Станки Эксперт.
6. Интехстрой.
7. Мирский, «Хирургия от древности до современности. Очерки истории.» (Москва, Наука, 2000, 798 с.).
8. Киржанова Е. А., Хуторянский В. В., Балабушевич Н. Г., Харенко А. В., Демина Н. Б. Методы анализа мукоадгезии: от фундаментальных исследований к практическому применению в разработке лекарственных форм. Разработка и регистрация лекарственных средств. 2014; 3(8): 66–80. DOI: 10.33380/2305-2066-2019-8-4-27-31.
9. З.С. Смирнова, Л.М. Борисова, М.П. Киселева и др. Противоопухолевая эффективность прототипа лекарственной формы соединения ЛХС-1208 для внутривенного введения // Российский биотерапевтический журнал. 2012. № 2. С. 49.
10. А.В. Ланцова, Е.В. Санарова, Н.А. Оборотова и др. Разработка технологии получения инъекционной лекарственной формы на основе отечественной субстанции производной индолокарбазола ЛХС-1208 // Российский биотерапевтический журнал. 2014. Т. 13. № 3. С. 25-32.