Закон Гука обычно не вызывает трудностей при изучении. Он утверждает, что деформация упругого тела пропорциональна приложенной силе, и это легко запомнить.
Для школьного курса этого знания достаточно, чтобы забыть о законе Гука. Однако, чтобы лучше его усвоить, стоит взглянуть на его портрет.
Если вы изучаете физику по углубленной программе или ваш преподаватель требует более глубокого понимания, этого знания будет недостаточно. При поступлении в технический институт его тоже не хватит. Закон Гука является основой для сопромата и важен при изучении механики.
Давайте изложим основные постулаты Гука в простой и понятной форме. Если у вас останутся вопросы, пишите их в комментариях или в личные сообщения.
Введение и основные понятия
Наверняка вы в детстве играли с луком и стрелами. Принцип работы этого устройства прост: согнутая палка, чаще всего из ивы, соединена тетивой, которая связывает её концы. Когда мы натягиваем тетиву стрелой, сила упругости палки заставляет её возвращаться в исходное состояние и передавать энергию стрелe.
Ключевое здесь — сила упругости. Это сила, возникающая при попытке изменить форму тела, то есть при его деформации. Она обусловлена внутренним взаимодействием частиц.
Также важно упомянуть о деформации, которая бывает обратимой (упругой) и необратимой. Закон Гука применим только к упругой деформации.
Упругая деформация — это такая деформация, после которой тело возвращается к своим первоначальным геометрическим характеристикам после снятия внешнего воздействия.
Простейшие виды деформации — растяжение и сжатие. Примером может служить пружина, о которой вы встретите упоминание в учебнике физики, где также будет представлен закон Гука.
Формулировка закона Гука
Закон формулируется так:
Деформация, возникающая в упругом теле, пропорциональна приложенной силе.
В виде формулы это можно записать следующим образом:
F = -kx ,
где F — сила упругости, k — коэффициент упругости, x — линейное изменение размеров тела.
Почему здесь минус? Его можно не указывать, если понимать логику. Сила — это вектор. Сила, возникающая в теле, направлена против силы, приложенной к нему, поэтому в формуле используется минус.
Иногда вместо k или x применяют другие обозначения, но смысл остается прежним.
Разбираемся с новыми буквами
У нас появилась сила упругости в теле, обозначаемая как F. По третьему закону Ньютона она равна векторной сумме сил, действующих на тело. Если, например, решаем задачу, где книга лежит на столе, а стол изгибается, то сила упругости в столе равна m*g, поскольку книга притягивается к полу и вызывает изгиб.
k — это жесткость тела, которая зависит от материала и его характеристик. Например, деревянная доска и железная труба имеют разную жесткость.
Эта величина расчетная, и в начале изучения вы будете брать её из таблиц как константу. Позже вам потребуется изучить модуль упругости первого рода, или модуль Юнга, что является основой сопротивления материалов.
x — это линейное удлинение, которое считается просто: новое значение минус старое. В более сложных случаях потребуется знание геометрии.
Новые важные понятия и обобщенный закон Гука
Обобщенный закон Гука требует отдельного рассмотрения. Здесь стоит отметить, что мы говорим только об одноосном деформировании. Мы работаем с пружиной, которую можно растянуть или сжать вдоль оси X. Но что, если пружина будет одновременно растягиваться и сгибаться?
Реальные тела обычно деформируются во всех направлениях, и в этом случае необходимо использовать обобщенный закон Гука. Для этого применяются тензоры. Это обширная тема, но важно помнить, что стандартный закон Гука применим только при деформации вдоль одной оси.
Также стоит упомянуть предел пропорциональности — максимальное механическое нагружение, при котором закон Гука остается в силе. На графике по оси Y откладывается механическое напряжение (в упрощении, сила), а по оси X — изменение размеров. Пока существует линейная зависимость, обозначенная красной прямой линией, закон Гука выполняется.
Разные материалы ведут себя по-разному. При достижении определенной точки некоторые тела могут сломаться, а другие — необратимо удлиниться или сжаться. Например, в одном случае тело деформировалось, но не сломалось, и связь между силой и деформацией стала нелинейной.
Закон Гука применим только при малых деформациях и не для всех материалов. Для многих полимеров он не работает. Напоминаем, что закон Гука актуален только для линейных систем.
Как описывать связь силы упругости и деформации в нелинейных системах, когда деформация значительная? Это сложная тема, и все сводится к обобщенному закону Гука с условием, что деформация мала. Однако при больших деформациях следует использовать другие методы расчета.
Сила упругости. Закон Гука
Сила упругости
Любое тело, подвергаясь деформации и внешнему воздействию, сопротивляется и стремится восстановить свою первоначальную форму и размеры. Это происходит из-за электромагнитного взаимодействия на молекулярном уровне.
Деформация — это изменение положения частиц тела относительно друг друга. В результате деформации изменяются межатомные расстояния и происходит перегруппировка атомных блоков.
Определение. Что такое сила упругости?
Сила упругости — это сила, возникающая при деформации тела и стремящаяся вернуть его в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие.
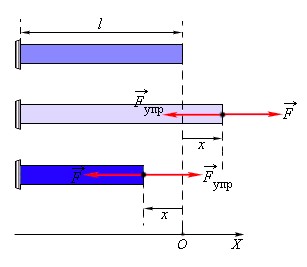
На рисунке показано, как действует сила упругости при сжатии или растяжении стержня.
Закон Гука
Для малых деформаций ( x ll l ) справедлив закон Гука.
Деформация в упругом теле пропорциональна приложенной силе:
[ F_{text{упр}} = -k x ]
где ( k ) — коэффициент жесткости. Единица измерения жесткости в системе СИ — Ньютон на метр. Жесткость зависит от материала, формы и размеров тела.
Знак минус указывает, что сила упругости противодействует внешней силе и стремится вернуть тело в исходное состояние.
Существуют и другие формулировки закона Гука. Относительная деформация тела определяется как:
[ varepsilon = frac{x}{l} ]
Напряжение в теле — это отношение:
[ sigma = -frac{F_{text{упр}}}{S} ]
где ( S ) — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука гласит, что относительная деформация пропорциональна напряжению:
[ varepsilon = frac{sigma}{E} ]
где ( E ) — модуль Юнга, который зависит только от свойств материала, а не от формы и размеров тела. Значение модуля Юнга для различных материалов варьируется: для стали ( E approx 2 cdot 10^{11} , text{Н/м}^2 ), для резины ( E approx 2 cdot 10^{6} , text{Н/м}^2 ).
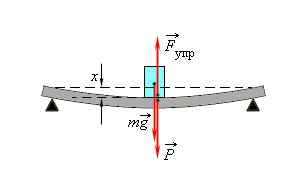
Закон Гука можно обобщить для сложных деформаций, например, при изгибе стержня. В этом случае сила упругости пропорциональна прогибу стержня.
Концы стержня опираются на две опоры, которые действуют на тело с силой ( vec{N} ), называемой силой нормальной реакции опоры. Эта сила направлена перпендикулярно (нормально) к поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции направлена вертикально вверх, уравновешивая силу тяжести.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, встречающийся как в теории, так и на практике. Пружины используются для измерения силы с помощью динамометра.
Динамометр — это пружина, растяжение которой проградуировано в единицах силы. Закон Гука применим к пружинам при значительных изменениях длины.
При сжатии и растяжении пружины действуют упругие силы, пропорциональные изменению длины пружины и ее жесткости (( k )).
В отличие от пружин, стержни и проволоки подчиняются закону Гука в узких пределах. При относительной деформации более 1% в материале возникают необратимые изменения — текучесть и разрушение.
ISopromat.ru
Законом Гука называют зависимость в механике, которая устанавливает связь между усилиями и упругими деформациями.
Этот закон был открыт в 1660 году английским ученым Робертом Гуком.
Проведя эксперименты с растяжением и сжатием пружин, Гук заметил, что изменение их длины пропорционально приложенной силе.
Он сформулировал это наблюдение: «Какова сила, таково и удлинение».
Современная формулировка закона отличается от оригинала и зависит от дисциплины, в которой рассматривается связь деформаций и усилий.
Подробнее о законе Гука смотрите в нашем видео:

Закон Гука в физике
В современных учебниках физики Закон Гука формулируется так:
«При малых деформациях сила упругости пропорциональна деформации тела и направлена в сторону, противоположную перемещению его частиц».
Коэффициент жесткости ( k ) зависит от размеров и материала образца.
Для стержней, работающих на растяжение или сжатие, его можно рассчитать по формуле:
[
k = frac{E cdot A}{l}
]
где:
- ( E ) — модуль упругости I рода (модуль Юнга);
- ( A ) — площадь поперечного сечения бруса;
- ( l ) — длина стержня.
Знак минус указывает на то, что силы упругого сопротивления направлены против растягивающей силы.
Закон Гука в сопромате
В технической механике, а именно в сопротивлении материалов, закон Гука утверждает: «До предела пропорциональности упругие деформации пропорциональны напряжениям».
Здесь:
- σ — нормальные напряжения в сечении;
- ε — относительные продольные деформации.
Рассмотрим преобразование закона в механическую форму.
Подставим вместо коэффициента k его выражение. Отношение продольной силы F к площади поперечного сечения A в левой части указывает на нормальные напряжения в сечении.
Отношение абсолютных деформаций к начальной длине образца представляет собой относительное изменение его длины.
Такой вид закона Гука применяется в сопротивлении материалов и технической механике. Он действует только при напряжениях, не превышающих предел пропорциональности.
При растяжении и сжатии
При растяжении и сжатии закон Гука можно выразить через геометрические параметры стержня, такие как длина и площадь поперечного сечения, в следующем виде, отражающем линейную деформацию:
Δl — абсолютная деформация стержня;
F — продольная сила;
l — длина стержня до нагружения;
E — модуль продольной упругости материала;
A — площадь поперечного сечения стержня.
При изгибе
При изгибе закон устанавливает зависимость между кривизной продольной оси и величиной изгибающего момента в сечении балки.
где:
ρ — радиус кривизны продольной оси балки в данном сечении;
M — величина внутреннего изгибающего момента;
E — модуль Юнга;
Ix — момент инерции поперечного сечения балки.
Обобщенный закон Гука
Для нагружения изотропных материалов, когда напряженное состояние отличается от линейного (одноосного), применяется обобщенный закон Гука.
- ε — относительные деформации вдоль осей;
- ν — коэффициент Пуассона;
- σ — нормальные напряжения на площадках элемента.
Деформации в поперечных направлениях также влияют на изменение продольных размеров.
Для чистого сдвига:
- γ — угловое перемещение площадки элемента;
- τ — касательные напряжения;
- G — модуль упругости II рода (модуль сдвига).
Испытание на растяжение >>
Диаграмма напряжений >>
Физика. 10 класс
Физика, 10 класс
- Закон Гука.
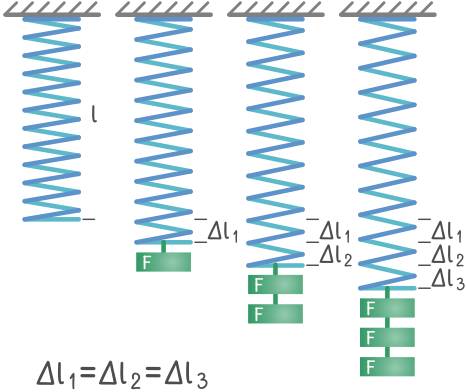
- Модели видов деформаций.
- Вычисление и измерение силы упругости, жёсткости и удлинения пружины.
Сила упругости — сила, возникающая в теле при его деформации и стремящаяся вернуть тело в исходное положение.
Деформация — изменение формы или размеров тела из-за неодинакового смещения его частей под воздействием другого тела. Виды деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
Закон Гука — сила упругости, возникающая при деформации тела (растяжение или сжатие пружины), пропорциональна удлинению тела и направлена в противоположную сторону перемещения частиц.
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика. 10 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2017, стр. 107-112.
- Рымкевич А.П. Сборник задач по физике. 10-11 класс. М.: Дрофа, 2009, стр. 28-29.
- ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
В нашем мире различные силы заставляют тела двигаться и взаимодействовать. Однако также наблюдаются разрушения, или деформации, сооружений: мостов, домов, машин.
Что нужно знать инженеру, чтобы строить надёжные конструкции? Почему деформации различны? Какие виды деформаций могут быть у конкретных тел? Почему одни тела восстанавливаются после деформации, а другие — нет? Как рассчитать величину этих деформаций?
Деформация — это изменение формы или размеров тела под воздействием другого тела. Почему деформации различны у разных тел при сжатии? Все вещества состоят из частиц, между которыми действуют силы взаимодействия электромагнитной природы. Эти силы проявляются как притяжение или отталкивание в зависимости от расстояния между частицами.
Сила упругости возникает при деформации любых тел, а также при сжатии жидкостей и газов. Она противодействует изменению формы тел.
Существуют несколько видов деформаций:
- При растяжении межмолекулярные расстояния увеличиваются. Это происходит, например, в струнах музыкальных инструментов и тросах.
- При сжатии межмолекулярные расстояния уменьшаются. Так деформируются стены и фундаменты зданий.
- При изгибе одни межмолекулярные слои увеличиваются, а другие уменьшаются. Это наблюдается в перекрытиях зданий и мостов.
- При кручении одни молекулярные слои поворачиваются относительно других. Так деформируются валы и пружины.
Первое научное исследование упругого растяжения и сжатия вещества провёл английский учёный Роберт Гук. Он установил, что при малых деформациях удлинение тела пропорционально приложенной силе:
[ F{text{упр}} = k cdot Delta ell = k cdot | ell — ell0 | ]
где:
— ( k ) — коэффициент жёсткости тела,
— ( ell0 ) — начальная длина,
— ( ell ) — конечная длина после деформации,
— ( Delta ell = | ell — ell0 | ) — абсолютное удлинение.
Единица измерения жёсткости в системе СИ — Н/м.
При больших деформациях изменение длины перестаёт быть пропорциональным приложенной силе, и слишком большие деформации могут разрушить тело.
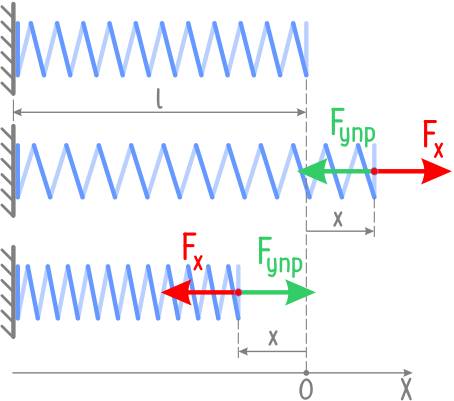
Для расчёта движения тел под действием силы упругости нужно учитывать направление этой силы. Если принять за начало отсчёта крайнюю точку недеформированного тела, то абсолютное удлинение можно охарактеризовать конечной координатой деформированного тела. При растяжении и сжатии сила упругости направлена противоположно смещению конца тела.
Закон Гука можно записать для проекции силы упругости на выбранную координатную ось:
[ F_{text{упр}, x} = — kx ]
где:
— ( x = Delta ell = ell — ell_0 ) — удлинение тела.
График зависимости модуля силы упругости от абсолютного удлинения тела представляет собой прямую, угол наклона которой зависит от коэффициента жёсткости ( k ). Если прямая круче, жёсткость больше; если уклон меньше, жёсткость меньше.
Важно помнить, что закон Гука выполняется только при малых деформациях. При больших деформациях изменение длины перестаёт быть пропорциональным приложенной силе.
- По результатам исследования построен график зависимости модуля силы упругости пружины от её деформации. Какова жёсткость пружины? Какое будет удлинение при подвешивании груза массой 2 кг?
Решение: По графику наблюдается линейная зависимость модуля силы упругости и удлинения пружины.
Зависимость физических величин по Закону Гука:
[ F_{text{упр}, x} = — kx ]
Зная, что ( F_t = mg = 20 , text{Н} ), получаем:
[ Ft = F{text{упр}} = k cdot Delta ell ]
Ответ: жёсткость пружины равна 200 Н/м, удлинение пружины равно 0,1 м.
-
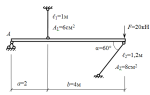
К системе из кубика массой 1 кг и двух пружин приложена постоянная горизонтальная сила. Система покоится. Левый край первой пружины прикреплён к стене. Удлинение первой пружины 0,05 м, её жёсткость равна 200 Н/м. Удлинение второй пружины 0,25 м.
-
Какова приложенная к системе сила?
- Какова жёсткость второй пружины?
- Во сколько раз жёсткость второй пружины меньше, чем первой?
Решение:
- Система находится в покое. Зная жёсткость и удлинение первой пружины, найдём силу, уравновешивающую приложенную силу:
[ F = F{text{упр}} = k1 cdot Delta ell_1 = 200 , text{Н/м} cdot 0,05 , text{м} = 10 , text{Н} ]
-
Жёсткость второй пружины:
-
( frac{k1}{k2} = frac{200}{40} = 5 )
Ответ: ( F = 10 , text{Н}; , k2 = 40 , text{Н/м}; , frac{k1}{k_2} = 5 ).
- Мустафин Р. И., Протасова А. А., Буховец А. В., Семина И. И. Исследование интерполимерных сочетаний на основе (мет)акрилатов в качестве перспективных носителей в поликомплексных системах для гастроретентивной доставки. Фармация. 2014; 5: 3–5.
- Смирнова З. С., Борисова Л. М., Киселева М. П. и др. Доклиническое изучение противоопухолевой активности производного индолокарбазола ЛХС-1208. Российский биотерапевтический журнал. 2014. № 1. С. 129.
- Мустафин Р. И., Протасова А. А., Буховец А. В., Семина И. И. Исследование интерполимерных сочетаний на основе (мет)акрилатов в качестве перспективных носителей в поликомплексных системах для гастроретентивной доставки. Фармация. 2014; 5: 3–5.
- Закон Гука в понятной форме.
- Сила упругости.
- Закон Гука.
- Конспект урока.
- ОФС.1.2.1.1.0003.15 Спектрофотометрия в ультрафиолетовой и видимой областях. Государственная фармакопея, XIII изд.



![Закон Гука [в понятной форме]](https://prime71.ru/blog/wp-content/cache/thumb/94/78bd457e6a4d794_320x200.jpg)