Рассмотренная диаграмма растяжения условна, так как значения нормальных напряжений σ = Р/F0 и относительных продольных деформаций ε = Δl/l0 откладываются на координатах. В процессе растяжения образца площадь сечения F0 и расчетная длина l0 изменяются. Поэтому фактические значения напряжений σ следует определять с учетом изменяющейся площади поперечного сечения Fист.
Деформацию ε также следует определять с учетом ее распределения по расчетной длине после начала образования шейки, где деформация концентрируется. В самом узком месте шейки малый отрезок dl имеет истинную деформацию. Однако определить истинную деформацию dΔl затруднительно, поэтому истинную относительную деформацию выражают через относительное остаточное сужение площади поперечного сечения образца.
Истинная диаграмма растяжения, показанная на рис. 3.12б, строится с учетом переменных поперечных размеров образца. Она проходит выше условной диаграммы после площадки текучести и заканчивается в точке D΄. В практических расчетах материал обычно работает при напряжениях, не превышающих предел текучести, поэтому истинная диаграмма имеет теоретическое значение и на практике не используется.
При сжатии также строят соответствующие диаграммы. В качестве металлических образцов используют цилиндры (рис. 3.15) с высотой h, равной диаметру d=20 мм. Для автоматических машин применяют образцы размером h=d=6 мм. Для других материалов используются кубические образцы: из дерева — а=50 мм; из цемента — а=70 мм; из бетона — а=200 или 300 мм.
Для сравнения рассмотрим диаграммы растяжения и сжатия для чугуна и стали, представленные на рис. 3.17. Начальные участки ОА диаграмм при растяжении и сжатии имеют одинаковый угол наклона к оси ε и одинаковую длину. Следовательно, модули упругости Е и пределы пропорциональности σпц при растяжении и сжатии совпадают. Однако при сжатии отсутствует ярко выраженная площадка текучести, поэтому пределы текучести σт считаются одинаковыми для растяжения и сжатия.
После площадки текучести при сжатии линия диаграммы постоянно возрастает, образец принимает бочкообразную форму и, наконец, расплющивается (рис. 3.15 б). Установить предел прочности σпч не удается, поэтому считается, что предел прочности при сжатии равен пределу прочности при растяжении. Такую форму имеют диаграммы растяжения алюминия и меди.
При растяжении образца из чугуна диаграмма имеет нелинейный характер с самого начала. Однако предел прочности σпч при сжатии превышает предел прочности σпч при растяжении. Для чугуна СЧ предел прочности σпч составляет 500 — 1500 МПа, что в 4-5 раз больше, чем при растяжении. Когда напряжения в образце приближаются к пределу прочности, в цилиндрическом образце, принявшем бочкообразную форму, появляются трещины под углом 45° из-за действия максимальных касательных напряжений τmax. Затем боковые части образца отделяются, и он приобретает форму двух конусов. При этом диаграмма сжатия обрывается.
Интересно поведение стального образца в упруго-пластическом состоянии, что соответствует участку CD (рис. 3.18). Если в некоторой точке М растянутый образец разгрузить, а затем подвергнуть цилиндрический образец деформации противоположного знака, то, как видно из диаграммы сжатия МА2С2, произойдет уменьшение значений предела пропорциональности до σ′пц и предела текучести до σ′т по сравнению с соответствующими величинами σпц и σт.
Таким образом, после наклепа при растяжении пределы пропорциональности и текучести при сжатии уменьшаются.
Эффект Баушингера — явление, связанное с понижением характеристик прочности металлов (предела пропорциональности, предела текучести) после растяжения и нагружения материала образца сжимающей нагрузкой. Этот эффект характеризует деформационную анизотропию стали и необходимо учитывать при исследовании упруго-пластического состояния элементов конструкций при сложных процессах нагружения.
Истинная диаграмма растяжения
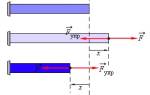
| Почти все механические характеристики, оценивающие свойства материала (см. пункт «Механические характеристики»), определяются относительно начальных размеров образца: площади A0 и длины l0. При этом не учитываются изменения размеров образца в процессе деформирования — уменьшение площади и увеличение длины. Это создает условность характеристик. Если преобразовать машинную диаграмму F — Δl в координаты «напряжение σ — относительная деформация ε» (σ = f(ε), рис. 1.2), то она в некотором масштабе повторит машинную диаграмму. Истинные напряжения S начинают отличаться от условных (технических) σ с первого момента нагружения, так как уменьшается площадь поперечного сечения образца. Истинная диаграмма растяжения S = φ(ε) является неубывающей. Существенные расхождения между диаграммами истинных и условных напряжений становятся заметными с началом пластической деформации (см. рис. 1.2). Считается, что до достижения максимальной нагрузки Fmax (см. рис. 1.2, напряжение σв) образец деформируется равномерно (см. рис. 1.2, сечение m): истинное напряжение Sm постоянно во всех сечениях, диаметр dm < d0 и одинаково по всей расчетной длине образца. На участке местного сужения в шейке (см. рис. 1.2, сечение n) минимальный диаметр образца значительно меньше начального (dn << d0). Истинные напряжения распределяются неравномерно по длине, как на участке упрочнения, и становятся значительно больше условных (Sn >> σn). В момент разрушения превышение Sк над σв может достигать 30–50 %. |
Рис. 1.2. Изменение конфигурации образца на различных стадиях деформирования (а); распределение истинных напряжений по длине образца при равномерном «m» и сосредоточенном «n» деформировании (б); диаграммы истинных S = φ(ε) и условных σ = f(ε) напряжений (в).
В научных целях обычно используют истинную диаграмму, построенную в координатах S — ψ или S — ε, где ψ — относительное сужение поперечного сечения (1.1); ε — относительная логарифмическая деформация ε = ln (ℓ/ℓ0). Истинная диаграмма более информативна и важна для понимания закономерностей сопротивления пластической деформации. Истинные напряжения точнее отражают поведение материала под нагрузкой, чем технические. Их используют в существующих и вновь создаваемых методиках расчета при сложном напряженном состоянии, действии циклических нагрузок и др.
Механические характеристики, оценивающие прочностные свойства материала, называются характеристиками прочности, а оценивающие пластические свойства — характеристиками пластичности.
К характеристикам прочности относятся:
— предел текучести физический;
— предел текучести условный;
— временное сопротивление (предел прочности);
— предел пропорциональности;
— предел упругости.
Предел текучести физический σт — напряжение, при котором образец деформируется без увеличения растягивающей нагрузки. Вычисляется по формуле:
σт = Fт / A0, (1.2)
где Fт — нагрузка, соответствующая площадке текучести (см. рис. 1.1); A0 — начальная площадь поперечного сечения образца.
Предел текучести условный σ0,2 — напряжение, при котором остаточное удлинение достигает 0,2 % от расчетной длины образца.
Порядок определения:
1. Рассчитать допуск на величину остаточного удлинения Δl0,2 = 0,002·ℓ0, где ℓ0 — начальная расчетная длина образца (база тензометра);
2. В масштабе оси деформаций машинной диаграммы отложить отрезок Δl0,2 (см. рис. 1.3, а);
3. Параллельно участку упругой деформации провести прямую до пересечения с диаграммой растяжения;
4. Измерить ординату F0,2 на диаграмме растяжения и вычислить нагрузку, соответствующую точке пересечения прямой с диаграммой;
5. Рассчитать условный предел текучести σ0,2 = F0,2 / A0. (1.3)
Временное сопротивление (предел прочности) σв — напряжение, соответствующее наибольшей нагрузке Fmax, предшествующей разрыву образца. Определяется делением усилия Fmax на первоначальную площадь поперечного сечения образца (см. рис. 1.1):
σв = Fmax / A0. (1.4)
Обратим внимание на характеристики сопротивления малым пластическим деформациям. Предел упругости — это наибольшее напряжение, до которого материал не получает остаточных деформаций. Предел пропорциональности — это наибольшее напряжение, превышение которого вызывает отклонение от закона Гука.
Рис. 1.3. Схемы к определению предела упругости и условного предела текучести (а), а также предела пропорциональности (б).
Анализ диаграмм растяжения, записанных с высокой точностью измерений, показывает, что отступление от закона Гука (прямой σ = E·ε) для многих материалов наступает на ранних стадиях нагружения. Поэтому численные значения пределов пропорциональности и упругости зависят от условно принятой степени приближения, с которой начальный участок можно рассматривать как прямую. Стандартом принято пределом пропорциональности считать напряжение, при котором «мгновенный» модуль упругости E = dσ/dε (модуль упругости в текущий момент испытания) уменьшается от своего начального значения на 50 %. Обе характеристики — предел упругости и предел пропорциональности — близки по смыслу и, как установлено Баушингером в 1879-1886 гг., различие между ними настолько мало, что в технических задачах их можно считать практически совпадающими.
Предел упругости σ0,05 — напряжение, при котором остаточное удлинение достигает 0,05 % длины участка рабочей части образца, равного базе тензометра.
Методика определения такая же, как и для условного предела текучести, но допуск на остаточную деформацию в 4 раза меньше (см. рис. 1.3, а).
σ0,05 = F0,05 / A0. (1.5)
Предел пропорциональности σпц — напряжение, при котором отклонение от линейной зависимости между нагрузкой и удлинением достигает такой величины, что тангенс угла наклона между касательной к кривой «нагрузка — удлинение» в точке Fпц и осью нагрузок увеличивается на 50 % от своего значения на упругом (линейном) участке.
Порядок определения:
1. На произвольной высоте диаграммы в пределах упругого участка проводят прямую mn, параллельную оси абсцисс (см. рис. 1.3, б);
2. Измеряют длину a отрезка mk между осью ординат и диаграммой растяжения; справа от диаграммы откладывают отрезок kn = a/2;
3. Из начала координат в точку n проводят луч 0n и параллельно ему касательную RT к диаграмме растяжения (при этом tgαпц будет на 50 % превышать tgα);
4. Ордината точки B касания с диаграммой определит искомую нагрузку Fпц. Предел пропорциональности вычисляют по формуле:
σпц = Fпц / A0. (1.6)
Истинное сопротивление разрыву Sк — напряжение, вычисляемое делением разрушающего усилия Fк (см. рис. 1.1, ордината точки D) на действительную площадь сечения в шейке Aк:
Sк = Fк / Aк. (1.7)
Площадь Aк вычисляется по диаметру dк (рис. 1.4). |
Литература:
- Patil H., Tiwari R. V., Repka M. A. Recent advancements in mucoadhesive floating drug delivery systems: A mini-review. Journal of Drug Delivery Science and Technology. 2016; 31: 65–71. DOI: 10.1016/j.jddst.2015.12.002.
- М.П. Киселева, З.С. Шпрах, Л.М. Борисова и др. Доклиническое изучение противоопухолевой активности производного N-гликозида индолокарбазола ЛХС-1208. Сообщение I // Российский биотерапевтический журнал. 2015. № 2. С. 71-77.
- Мирский, «Хирургия от древности до современности. Очерки истории.» (Москва, Наука, 2000, 798 с.).
- https://studopedia.net/1037075ponyatie-ob-istinnoy-diagramme-rastyazheniya.html.
- https://lektsia.com/1x7e4f.html.
- https://lfirmal.com/istinnaya-diagramma-rastyazheniya/.
- https://cyberpedia.su/12x102fb.html.
- А.В. Ланцова, Е.В. Санарова, Н.А. Оборотова и др. Разработка технологии получения инъекционной лекарственной формы на основе отечественной субстанции производной индолокарбазола ЛХС-1208 // Российский биотерапевтический журнал. 2014. Т. 13. № 3. С. 25-32.
- М.П. Киселева, З.С. Шпрах, Л.М. Борисова и др. Доклиническое изучение противоопухолевой активности производного N-гликозида индолокарбазола ЛХС-1208. Сообщение I // Российский биотерапевтический журнал. 2015. № 2. С. 71-77.
- Sprengel, «Pragmatische Geschichte der Heilkunde».