Решение двухмерной магнитостатической задачи методом конечных элементов (линии и цвет показывают направление и величину магнитной индукции).

Разбиение на конечные элементы позволяет изменять размер элементов: уменьшать его вблизи интересующей области и увеличивать для снижения затрат процессорного времени.

Метод конечных элементов (МКЭ) — численный метод для решения дифференциальных уравнений с частными производными и интегральных уравнений, возникающих в прикладной физике. Он широко применяется в механике деформируемого твёрдого тела, теплообмене, гидродинамике, электродинамике и топологической оптимизации.

Идея метода[править | править код]

Суть метода заключается в его названии. Область поиска решения дифференциальных уравнений делится на конечное количество элементов. В каждом элементе выбирается форма аппроксимирующей функции, чаще всего полином первой степени. Вне элемента эта функция равна нулю. Значения функций на границах элементов (в узлах) являются искомыми и заранее неизвестны. Коэффициенты аппроксимирующих функций определяются условием равенства значений соседних функций на границах элементов. Эти коэффициенты выражаются через значения функций в узлах, что приводит к системе линейных алгебраических уравнений. Количество уравнений соответствует количеству неизвестных значений в узлах и пропорционально количеству элементов, ограничиваясь возможностями ЭВМ. Поскольку каждый элемент связан с ограниченным числом соседей, система линейных уравнений имеет разрежённый вид, что упрощает её решение.

В матричных терминах формируются матрицы жёсткости (или матрица Дирихле) и масс. На эти матрицы накладываются граничные условия: при условиях Неймана матрицы остаются неизменными, а при условиях Дирихле из них исключаются строки и столбцы, соответствующие граничным узлам, так как значения этих компонентов решения известны. Затем собирается система линейных уравнений и решается одним из известных методов.

С точки зрения вычислительной математики, идея метода конечных элементов заключается в минимизации функционала вариационной задачи на множестве функций, каждая из которых определена на своей подобласти.

Метод широко применяется в проектировании сооружений и моделировании движения, например, грунта. За границей он быстро получил распространение, в то время как в России начал использоваться только в 2000-х годах, заменив вариационно-разностные и конечно-разностные методы.

Среди недостатков метода можно отметить влияние размера сетки на конечные результаты.

Иллюстрация метода на одномерном примере[править | править код]

Функция с нулевыми значениями на концах (голубая) и её аппроксимация отрезками (красная).

Базисные функции ( v_k ) (голубые) и линейная комбинация из них, аппроксимирующая искомую функцию (красная).

Визуализация деформации машины при асимметричном ударе с использованием метода конечных элементов.

Рассмотрим одномерное пространство ( R^1 ) и решим дифференциальное уравнение для нахождения функции на промежутке от 0 до 1. На границах области значение функции равно 0:

где известная функция, неизвестная функция от ( x ), и вторая производная от ( u ) по ( x ). Решение задачи методом конечных элементов разбивается на два этапа:

1. Переформулируем граничную задачу в слабую (вариационную) форму. На этом этапе вычисления минимальны.
2. Разобьём слабую форму на конечные отрезки-элементы.

Это приводит к системе линейных алгебраических уравнений, решение которой аппроксимирует искомую функцию.

Если существует решение, то для любой гладкой функции ( u ), удовлетворяющей граничным условиям в точках ( a ) и ( b ), можно записать следующее выражение:

[
(1)
]

С помощью интегрирования по частям преобразуем выражение (1) в следующую форму:

[
(2)
]

Это преобразование выполнено с учётом того, что ( u(a) = u(b) = 0 ).

Разобьём область, в которой ищется решение, на конечные промежутки, и получим новое пространство:

[
(3)
]

где кусочная область пространства. Существует множество способов выбора базиса. Выберем базисные функции, представляющиеся прямыми линиями (полиномами первой степени):

для ( x in [0, 1] ).

Теперь, если представить искомое приближённое решение в виде ( u_h ), а функцию аппроксимировать как ( u ), то с помощью (3) можно получить следующую систему уравнений относительно искомых коэффициентов:

[
A cdot u = b,
]

где ( A ) — матрица системы, а ( b ) — вектор правой части.

Преимущества и недостатки[править | править код]

Метод конечных элементов (МКЭ) сложнее в реализации, чем метод конечных разностей. Однако у МКЭ есть ряд преимуществ, которые проявляются в реальных задачах: он позволяет обрабатывать области произвольной формы и создавать более редкие сетки в местах, где высокая точность не требуется.

Долгое время распространению МКЭ мешало отсутствие алгоритмов для автоматического разбиения области на «почти равносторонние» треугольники. Погрешность, в зависимости от вариации метода, обратно пропорциональна синусу самого острого или самого тупого угла в разбиении. Тем не менее, эту задачу удалось решить с помощью алгоритмов триангуляции Делоне, что позволило создавать полностью автоматические системы автоматизированного проектирования (САПР) на основе метода конечных элементов.

История развития метода[править | править код]

Метод конечных элементов (МКЭ) возник в 1930-х годах для решения задач строительной механики и теории упругости. Основоположниками идей МКЭ считаются Александр Хренников и Рихард Курант, чьи работы были опубликованы в 1940-х. В 1944 году Иоаннис Аргирис впервые продемонстрировал эффективность МКЭ, применив его с помощью ЭВМ.

В 1950-х годах в Китае Кан Фэн предложил численный метод для решения дифференциальных уравнений в частных производных, предназначенный для расчета плотин. Этот метод, основанный на вариационном принципе, стал известен как метод конечных разностей и может рассматриваться как независимая реализация МКЭ.

Несмотря на различия в деталях, все эти подходы объединяет дискретизация непрерывной области сеткой, состоящей из дискретных поддоменов, называемых элементами.

Дальнейшее развитие МКЭ связано с задачами космических исследований в 1950-х годах. В СССР метод получил распространение в 1960-х благодаря Леонарду Оганесяну.

В 1963 году МКЭ получил новый импульс после доказательства его связи с методом Рэлея — Ритца, который минимизирует потенциальную энергию и сводит задачу к системе линейных уравнений равновесия. Установление этой связи позволило применять МКЭ к задачам, описываемым уравнениями Лапласа и Пуассона. В 1968 году было показано, что уравнения для элементов можно получать с помощью метода взвешенных невязок, таких как метод Галёркина или метод наименьших квадратов. Это значительно расширило область применения МКЭ, превратив его в общий метод численного решения дифференциальных уравнений.

С развитием вычислительных технологий возможности МКЭ продолжают расширяться, что позволяет решать все более широкий класс задач. В настоящее время существует множество реализаций метода для моделирования процессов диффузии, теплопроводности, гидродинамики, механики, электродинамики и других областей.

См. также[править | править код]

• Метод дискретных элементов
• Метод конечных разностей
• Метод конечных объемов
• Метод подвижных клеточных автоматов
• Метод граничных элементов

Литература[править | править код]

• Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. — М.: Мир, 1984.
• Деклу Ж. Метод конечных элементов: Пер. с франц. — М.: Мир, 1976.
• Зенкевич О. Метод конечных элементов в технике. — М.: Мир, 1975.
• Зенкевич О., Морган К. Конечные элементы и аппроксимация: Пер. с англ. — М.: Мир, 1986.
• Сегерлинд Л. Применение метода конечных элементов. — М.: Мир, 1979. — 392 с.

Ссылки[править | править код]

Боровков А.И. и др. Компьютерный инжиниринг. Аналитический обзор — учебное пособие. — Санкт-Петербург: Издательство Политехнического университета, 2012. — 93 с. — ISBN 978-5-7422-3766-2.

Примечания[править | править код]

Лекция третья. Введение в Метод конечных элементов (МКЭ)

Лекция третья. Введение в МКЭ

«Не пора ли, друзья мои, нам замахнуться на Вильяма, понимаете ли, нашего Шекспира?»

Из первых двух лекций мы узнали о методе конечных элементов (МКЭ), который эффективно применяется для расчетов деформаций различных объектов, таких как консервные банки и автомобили. Читателю необходимо понять, как работает этот метод. Поскольку аудитория лекций состоит не только из математиков и механиков, но и из финансистов, юристов и автоэкспертов, мы будем рассматривать МКЭ в простой форме, обозначая ключевые проблемы.

Рассмотрим задачу нахождения зависимости y от x в интервале от a до b. Существует два подхода: 1) искать аналитическую зависимость в виде функции y=y(x), как это делали в школе при интегрировании, или 2) представлять функцию в виде набора точек с заданной точностью.

На рисунке выше показана искомая функция y=y(x), для которой найдена ломаная 1-2-3-4-5-6, что не сильно снижает точность. Чем больше точек мы используем для представления функции, тем точнее будет результат. Методы, которые находят функцию в виде конечного числа точек, называются численными.

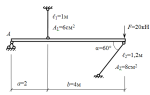
Решим простую, но реальную задачу. Необходимо рассчитать упругий изгиб элемента конструкции с прямой формой, один конец которого жестко закреплен, а другой отогнут вниз под действием силы, как показано на рисунке. Таким элементом может быть консольная балка, стойка автомобиля или продольное сечение капота.

На рисунке выше балка разбита на два конечных элемента: первый с узлами 1 и 2, второй — с узлами 2 и 3. Узел 2 является общим для соседних элементов.

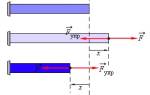
Перед решением задачи необходимо понять свойства конечного элемента. Рассмотрим абстрактный конечный элемент с узлами i и j.

Конечным элементом называется часть конструкции, перемещения любой точки которой можно выразить через перемещения узлов без значительного ущерба для точности. При изгибе каждая точка конечного элемента с узлами i и j имеет две степени свободы:

1) перемещение по вертикали на расстояние v,
2) разворот поперечного сечения на угол Ө.

Поскольку конечный элемент представлен двумя узлами, он имеет четыре степени свободы. Функцию перемещения в каждой точке с координатой x внутри элемента можно представить полиномом с четырьмя коэффициентами.

Почему полином? Это проще. Мы представили функцию y(x) внутри каждого конечного элемента отрезком прямой и убедились в достаточной точности. Если нужна большая точность, можно увеличить количество конечных элементов.

Из сопромата известно, что функция угла разворота сечения является первой производной от функции перемещения.

Положим, что начало системы координат расположено в узле i, а ось x направлена вправо. Выразим коэффициенты полинома через перемещения узлов i и j: vi, Өi, vj и Өj.

При x=0 (в узле i):

В узле j (при x=xj=l, где l=xj-xi — длина конечного элемента):

Решая эту систему уравнений, получаем выражение для перемещения в любой точке конечного элемента через перемещения в его узлах. Зная длину элемента l и перемещения в узлах, мы можем найти перемещение в любой точке.

Запишем это в матричном виде. Введем вектор узловых перемещений конечного элемента и вектор формы элемента. Тогда выражение для перемещения можно компактно записать.

Теперь определим, что подразумевается под словом «деформация». В английском языке «деформация» (deformation) и «деформация» (strain) имеют разные значения. Первое обозначает изменение геометрии, второе — меру деформации.

Рассмотрим образец материала с начальной длиной L0. Если его растянуть, увеличив длину на величину, степень деформации будет безразмерной величиной.

Эта величина называется деформацией или относительной деформацией. Однако относительная деформация не аддитивна — при сложении возникают ошибки. Например, если образец длиной 10 см растянули на 1 см, получаем деформацию 1/10. Если затем его растянуть еще на 1 см, получаем деформацию 1/11. Суммарная относительная деформация будет меньше 2/10.

Для нашей задачи оставим прежнее определение относительной деформации, которое корректно для малых деформаций.

Конструкция имеет некоторую толщину, постоянную по длине конечного элемента. Малый фрагмент элемента до и после изгиба показан на рисунке. При изгибе длина волокна АВ не изменяется, а радиус кривизны составит . Относительная деформация произвольного волокна CD равна.

Из математики известна зависимость для малых углов разворота сечения.

Согласно закону Гука напряжения связаны с деформациями через модуль упругости (модуль Юнга).

Известно, что изгибающий момент связан с напряжениями в сечении, учитывая момент инерции сечения.

Теперь у нас есть вектор узловых перемещений, вектор узловых сил, вектор относительных деформаций и вектор напряжений в сечении. Эти векторы выражаются через компоненты вектора перемещений, которые являются неизвестными задачи.

Если к узлам сетки конечных элементов приложить внешние силы или задать им известные перемещения, истинные перемещения остальных узлов будут такими, которые обеспечивают минимум полной энергии деформации.

Минимизация полной энергии равносильна решению системы дифференциальных уравнений, описывающих деформацию балки.

Как вычислить полную энергию? Произведение напряжений на соответствующие деформации дает удельную энергию деформации. Чтобы вычислить энергию по всему объему конечного элемента, нужно проинтегрировать удельную энергию по объему и просуммировать по всем элементам. Полная энергия деформации — это разность энергии всех конечных элементов и работы внешних сил. Чтобы найти минимум, нужно записать выражение для полной энергии и продифференцировать его по каждому перемещению. Это даст систему линейных уравнений.

Вид последней формулы показывает, что энергия деформации равна работе внешних сил.

Выражение для матрицы жесткости конечного элемента следующее.

Матрица жесткости имеет размер 4х4 и симметрична относительно главной диагонали. Структуру этой матрицы можно представить в виде подматриц.

Аналогично структуру вектора перемещений и вектора узловых сил можно представить в виде подвекторов.

Теперь начнем решать реальную задачу. Пусть конечный элемент №1 имеет узлы 1 и 2 с координатами, а конечный элемент №2 — узлы 2 и 3. Длина l=100 мм одинакова для обоих элементов. Для обоих примем модуль упругости и момент инерции сечения.

Вычисляем компоненты матрицы жесткости первого и второго конечных элементов, они будут одинаковы.

Далее распределяем подматрицы по глобальной матрице жесткости и суммируем.

Получаем глобальную матрицу жесткости размером 6х6.

Узловые силы пока не заданы, и глобальный вектор узловых сил заполнен нулями.

Имея неизвестный глобальный вектор узловых перемещений, получаем систему линейных уравнений.

В узле №1 имеется жесткое закрепление балки, т.е. перемещение и угол разворота равны нулю. Обнуляем первую и вторую строки и столбцы матрицы жесткости, ставим на главной диагонали по 1.

Теперь из решения системы уравнений всегда будет .

Зададим перемещение узла №3 вниз на 10 мм. Для этого сформируем вектор.

Теперь можно решать систему уравнений. Решение даст узловые перемещения.

Теперь, когда узловые перемещения найдены, можно подставить их в формулу для перемещения v и построить график — форму деформированной балки.

С аналитическим решением совпадение будет на 100%, так как упругая линия балки описывается уравнением третьей степени.

В результате у нас осталось три неизвестных — перемещение и угол разворота в узле №2, угол разворота в узле №3. Эти неизвестные обеспечивают минимум затрат энергии на деформацию.

МКЭ может использоваться для судебной экспертизы ДТП — чем точнее обмер деформированного автомобиля, тем точнее результат. Недостаток данных приведет к расчету возможной наименьшей величины затраченной на деформацию энергии.

Судебные автоэксперты могут быть удивлены новыми знаниями. Не стоит впадать в ступор — всему можно научиться.

Часто задают вопрос: «По какой формуле Вы сделали расчет?». Ответ: , причем всегда и для всех ДТП.

В.Н. Никонов,

ведущий научный сотрудник Института механики Уфимского научного центра РАН,

кандидат технических наук

Статья в формате PDF

Смотри далее, лекция № 4

© 2007, ЦНЭАТ, г. Самара, ссылка на ЦНЭАТ и страницу обязательны (www.cneat.ru)

Литература:

1. ОФС.1.2.1.2.0003.15 Тонкослойная хроматография // Государственная фармакопея, XIII изд.
2. Мирский, «Медицина России X—XX веков» (Москва, РОССПЭН, 2005, 632 с.).
3. ОФС.1.2.1.1.0003.15 Спектрофотометрия в ультрафиолетовой и видимой областях // Государственная фармакопея, XIII изд.
4. https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%BA%D0%BE%D0%BD%D0%B5%D1%87%D0%BD%D1%8B%D1%85_%D1%8D%D0%BB%D0%B5%D0%BC%D0%B5%D0%BD%D1%82%D0%BE%D0%B2.
5. https://cneat.ru/lex3.html.
6. З.С. Смирнова, Л.М. Борисова, М.П. Киселева и др. Противоопухолевая эффективность прототипа лекарственной формы соединения ЛХС-1208 для внутривенного введения // Российский биотерапевтический журнал. 2012. № 2. С. 49.
7. А.В. Ланцова, Е.В. Санарова, Н.А. Оборотова и др. Разработка технологии получения инъекционной лекарственной формы на основе отечественной субстанции производной индолокарбазола ЛХС-1208 // Российский биотерапевтический журнал. 2014. Т. 13. № 3. С. 25-32.
8. Bangun H., Aulia F., Arianto A., Nainggolan M. Preparation of mucoadhesive gastroretentive drug delivery system of alginate beads containing turmeric extract and anti-gastric ulcer activity. Asian Journal of Pharmaceutical and Clinical Research. 2019; 12(1):316–320. DOI: 10.22159/ajpcr.2019.v12i1.29715.